Topologische grootheden stromen
Topologie is in opkomst binnen veel wetenschappelijke disciplines. Het stond zelfs aan de basis van de Nobelprijs voor de Natuurkunde in 2016. Leids fysicus Marcello Caio en zijn collega's hebben nu het bestaan ontdekt van topologische stroom, naar analogie met elektrische stroom. Publicatie op 14 januari in Nature Physics.
We zijn gewend om eigenschappen toe te kennen aan voorwerpen, zoals kleur, temperatuur of fase—gas, vloeibaar of vast. Dat kunnen we doen voor elk klein stukje van ieder object. Als iemand vraagt naar een specifiek punt op een donut, kun je antwoorden dat het bruin, vast en op kamertemperatuur is. Topologische eigenschappen zijn anders. Ze bevatten informatie over het gehele object. Een donut heeft bijvoorbeeld één gat. Het is onmogelijk om het aantal gaten te tellen door te focussen op een specifiek deel van de donut. Je moet het in zijn geheel beschouwen. Topologie is tegenwoordig een belangrijk onderdeel van veel onderzoeksgebieden. In 2016 werd bijvoorbeeld de Nobelprijs voor de Natuurkunde toegekend voor onderzoek aan topologie.
Chern index
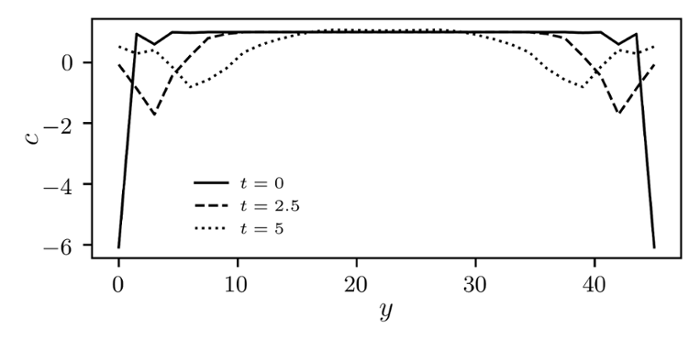
De zogenoemde Chern index is een andere, hoewel erg abstracte, topologische grootheid. Dit betreft een speciaal geval binnen de topologie. Kort geleden ontdekten wetenschappers dat de Chern index een dichtheid heeft, en noemden die Chern marker. Daarmee kun je de topologie van een compleet systeem te weten komen door alleen maar op lokaal niveau te kijken. De vaste lijn in figuur 1 toont de ruimtelijke verdeling van Chern marker, waar elk lokaal punt zijn eigen waarde heeft. (Bedenk dat deze grafiek absurd zou zijn voor een algemene eigenschap zoals het aantal gaten in een object.) De lokale punten moeten zich wel aan één regel houden op algemeen niveau: het gemiddelde van alle lokale waardes moet altijd nul zijn.
Topologische stroom
Leids natuurkundige Marcello Caio en een groep wetenschappers uit het Verenigd Koninkrijk hebben nu ontdekt dat als je een systeem verstoort, de lokale Chern waardes zich zullen verdelen door vanaf de randen naar het midden te vloeien. Ter vergelijking: algemene topologische eigenschappen zijn robuust tegen verstoringen—het aantal gaten in een donut verandert alleen bij een drastische gebeurtenis, zoals een grote hap. In figuur 1 zorgt een verstoring ervoor dat de grafiek zich hervormt om aan de voorwaarde te blijven voldoen dat zijn integraal nul moet zijn. Caio en zijn collega’s ontdekten dat dit niet instantaan gebeurt, en dat er dus een stroom van Chern marker door het systeem vloeit. Dit kun je zien als een topologische stroom, naar analogie met een conventionele elektrische stroom.
Nieuwe apparaten
Caio: ‘In de verre toekomst zou dit kunnen leiden tot nieuwe apparaten op basis van topologische stroom als aanvulling op elektrische stroom. Je kunt hier op veel vlakken onderzoek naar doen. Zijn er andere manieren om deze stroom te creëren? Kunnen we de stroom sturen? Er zijn veel spannende mogelijkheden.’
Publicatie
M. D. Caio, G. Möller, N. R. Cooper, and M. J. Bhaseen, ‘Topological Marker Currents in Chern Insulators’, Nature Physics