Research project
Language and number
Knowledge and culture subproject 2: "Language and number" of Leiden University Centre for Linguistics
- Duration
- 2013 - 2017
- Contact
- Johan Rooryck
- Funding
-
 NWO Horizon grant
NWO Horizon grant
This project investigates the mapping between the core knowledge system for number and the faculty of language. The central research question is how linguistic investigations of number can shed new light on our understanding of the core knowledge system for number.
Recent research shows that the core knowledge system of number consists of two nonverbal subsystems that are present in both newborn infants and animals (Spelke 2011).
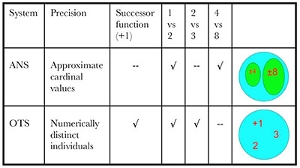
The first subsystem, the Approximate Number System (ANS) compares the numerosities of distinct sets without individuating their members. This system is imprecise and ratio-sensitive. Initially, it only distinguishes between sets with a ratio of 2 or higher (e.g. 4 vs. 8), the ratio decreasing with maturation (Dehaene 1997).
The second subsystem, the Object Tracking System (OTS) yields representations of small numbers of objects, i.e. 1 to 3 (perhaps 4). It does not work on sets larger than 4. OTS is also different from ANS in that it is precise, able to distinguish between 2 and 3, and sensitive to adding or subtracting one individual.
The limits of the two number systems are overcome when the child starts using cardinal numerals such as one, two, three, and acquires the counting principle. ANS and OTS are the foundation for symbolic mathematics. Spelke (2011) suggests that the language faculty plays a crucial role in integrating the two systems.
In line with the program set out by Carey (1998), this project adopts two methods to study the mapping between the core system of number and the faculty of language: (i) cross-linguistic comparisons to elucidate universal and variable properties of the systems (project 5.2); (ii) comparisons over development of the systems in the child, and their changes with growth and education (project 5.3). The results of these projects will provide crucial input for other lines of research in the field of the core knowledge systems (Spelke 2011), including cross-cultural comparisons (e.g., Pica et al. 2004, 2006). The data collected in these projects will be made available on-line (WALS for the typological data; CHILDES for the acquisition data).
Postdoc project (Lisa Bylinina): Number in language: a typological study
For the implementation of this subproject, see Lisa Bylinina's page.
This project studies the relation between the properties of the core knowledge system for number and the linguistic properties of numerals in the world’s languages. The project focuses on the following questions:
(1) a. Does the distinction between OTS and ANS manifest itself in
the numeral systems of the languages of the world, and if so, how?
b. What does the special linguistic status of 1 as opposed to
all other numerals tell us about OTS and ANS?
Linguistic evidence suggests that the split between OTS and ANS is reflected in the language system. Crosslinguistically, 1 to 3 (or 4) have linguistic properties that are different from those of the higher numbers (Hurford 1987): (i) no language has grammatical trial number unless it has dual number, and languages that distinguish a grammatical number higher than 3 are rare or non-existent (Greenberg 1963); (ii) ordinal suppletion (first instead of regular one-th, second instead of two-th) is cross-linguistically common but largely restricted to ordinals below fourth (Veselinova 1998; Stolz & Veselinova 2011); (iii) cross-linguistically, the words for 1 to 3 agree in gender and case with the noun, unlike numerals higher than 3.
Studies on OTS do not attribute a special status to 1 vs. 2 and 3. However, linguistically the numeral 1 is distinct from all other cardinal numerals in many languages. In Hebrew, the word for 1 follows the noun while all other cardinal numerals precede it (Borer 2005). In Dutch, 1 is morphosyntactically distinct from the other cardinal numerals: it allows derivation with -heid ‘-ity’; but not with -tal ‘-some’; it can be modified by zo ‘so’, hoe‘how’ and te ‘too’; and it is incompatible with EACH and EVERY (Barbiers 2007). In many languages, 1 has more in common with indefinite numerals such as MANY and FEW than with the cardinal numerals. Ordinals can be regularly derived from numerals, but 1, MANY and FEW block regular ordinal formation. As such, the behavior of 1 is surprisingly more similar to the approximate number properties of ANS than with the numerically distinct values of OTS. Children acquiring language first distinguish 1 from all other numerals (Spelke 2011). The project will therefore investigate the relation between the special linguistic status of 1 with respect to the core knowledge subsystems of ANS and OTS. The linguistic behavior of 1 might support Piazza’s (2010) conclusions on the basis of neuroimaging techniques that OTS is not a proper subsystem of number in its own right.
Importantly, the grammatical properties distinguishing ANS from OTS, and 1 from the other numerals, have not yet been systematically studied for a properly representative sample of the world’s languages. This project will provide a more complete cross-linguistic typology of the morphosyntactic properties of cardinal numerals and quantifiers such as many and few. The study will include properties such as ordinal suppletion, inflection, case, derivational properties, syntactic distribution, modifiability and predicative use. A model will be provided to capture the linguistic similarities and differences between the numeral categories in terms of feature composition (see Barbiers 2007 and Harbour 2011). Distinct behavior of the numeral categories under the influence of the core knowledge system for number is expected to show up in all languages.
The primary data source for this study is the World Atlas of Linguistic Structures (Dryer & Haspelmath 2011, Comrie 2011), which currently contains 2678 languages in 510 genera and 212 families, including relevant features for ordinal numerals (321 languages) and order of numeral and noun (1154 languages). Starting from these data we will select at least one language from each genus, completing the inventory with reference grammars and data elicitation.
PhD project (Caitlin Meyer): The acquisition of numerals and ordinals
For the implementation of this subproject, see Caitlin Meyer's page.
This project investigates the acquisition of numerals in relation to the development of the core knowledge system for number. The following research questions will be investigated:
(2) a. What is the sequence of acquisition for (the morphosyntactic
properties of) 1, the other numerals, and quantifiers such as MANY?
b. How are words for ordinals acquired by children?
c. How is the numeral for 2 acquired by children?
Language acquisition experiments (Gelman & Gallistel 1978, Feigenson & Carey 2005, Le Corre & Carey 2007) show that two-year-old children who can count from 1 to 10 start with a distinction between numeral 1 and all other numerals. In give-a-number-tasks they give the experimenter one object when asked for one, for all other numerals they give a random number of objects but never one. The next numeral acquired is 2, then 3 and then the other cardinal numerals. If MANY has more properties in common with 1 than with the other cardinals (cf. §5.2), it is expected that MANY is acquired after 1 but before the other cardinals. The first goal of this subproject is to test this expectation, and to investigate the acquisition of the specific morphosyntactic properties of 1, 2, 3 and quantifiers such as MANY and FEW.
The second goal is to study the acquisition of ordinals. Ordinals are often morphologically or syntactically derived from numeral stems. Their compositional complexity suggests that they are acquired after numerals. In many languages, ordinal formation adds a definite article or suffix to the cardinal. This has the semantic effect of picking out one discourse-anchored ordering of the set of orderings defined by the corresponding cardinal. We therefore expect ordinal formation to be acquired either simultaneously or after the acquisition of the definite article. The acquisition order of ordinals might be sensitive to the split between OTS and ANS. Since 1 is acquired before 2 which is acquired before the other numerals, the order of ordinal acquisition should be: FIRST - SECOND - THIRD etc., unless acquisition of ordinals comes in after the acquisition of the cardinals from 1 to 10. Interference with ordinal suppletion will also be investigated. As ordinal suppletion is restricted to OTS, the question arises what happens to suppletive forms in child language. In the acquisition of irregular verb forms, children go through various stages: correct irregular form (e.g. ate) > incorrect regular (i.e. overgeneralized) form; (eated) > mixtures (ated) > correct form (ate). Does something similar happen with suppletive ordinals, i.e. do we find overgeneralization of regular ordinal formation for 1, 2 and MANY?
The third goal of this subproject is to investigate the acquisition of 2. Children go through a short stage where they use 2 but not the higher cardinals. 2 must therefore have special properties. Cross-linguistically this is confirmed by words such as PAIR, COUPLE and DUO. Our hypothesis is that children in the 2-stage initially take 2 to refer to a unit consisting of two parts rather than to a set of two elements. We expect children to apply 2 to twofold units first, e.g. shoes, eyes, before generalizing it to all sets of two elements. If 2 does not yet belong to the set of cardinal numerals at this stage, the child cannot have the regular ordinal such as Dutch twee-de ‘second’, if s/he has ordinals at all.
A pilot study of the CHILDES database shows that there are relatively few occurrences of cardinal and ordinal numerals in naturally occurring child language data. The ordinal system is acquired relatively late. These findings imply that the design of this project should include elicitation, perception, and judgment experiments involving children from age 2 until (at least) 8. Therefore a mixed longitudinal and cross-sectional study will be carried out in years 2-3 of the project including 3 groups of 25 Dutch children, ages 2-3, 4-5, 6-7, possibly extending to a fourth group age 8-9. While any language would in principle qualify, we choose Dutch because its morphosyntax has been well studied (e.g. Unsworth & Hulk (2010) for gender; Blom, Polišenská & Weerman (2006/7) for agreement; van Wijk (2007) for the plural; Veenstra et al. (2010) for quantitative er; Keij et al. (2012) for determiners). Experimental protocols will be developed on the basis of previous research, replicating these settings as closely as possible, and augmenting them for the investigation of their distinctive morphosyntactic properties.
