Leiden scientists develop topological barcodes for folded molecules
The team of Alireza Mashaghi at the Leiden Academic Centre for Drug Research has found a way to determine and classify the shape of proteins. Their new theory defines the topology of proteins as a simple and precise barcode that allows the identification of all types of folds. ‘This barcode enables among others more profound research into diseases caused by misfolding proteins, such as neuromuscular diseases and some sorts of cancer.’
Tying knots
‘We are all familiar with tying a rope into a knot,’ tells Mashaghi. ‘Just like that, molecular chains in our cells are folded into proteins and genes. Our goal was to find a way to describe these knots in a mathematical way, to describe the topology (see text box below) of proteins.’ About half a century ago, Nobel Prize winner Linus Pauling, predicted that one day it would become clear that this topology of biological molecules is as important in determining the physiological properties as the chemical structure of molecules. He also predicted that this insight would lead to great advances in biology and medicine.
Mathematicians have been studying the mathematics behind knots since 1833. Since then, the field of ‘knot theory’ has become one of the most important fields of mathematics, with many applications in physics and chemistry. But although mathematicians were able to study and classify the entanglement of chains such as ropes, their theory could not yet explain the topology of proteins. ‘There has not even been a definition for it,’ adds Mashaghi.

Sticky and unraveling knots
Still, scientists did study and describe the geometry of the folded molecules with great precision. Scientific advances such as the invention of crystallographic methods and spectroscopy have made it possible to measure things as the exact location of each atom or the bending curvature of the protein chain. But the topology is a different story. Alireza gives two main reasons for this. ‘The first is that unlike ropes, proteins are sticky. This creates connections within the protein chain between certain points.’
‘Secondly, if we hold and pull the two ends of a protein like an intertwined rope, the proteins will unravel and in more than 97 per cent of the cases, no knots will be left. According to the conventional knot theory, this means that all these proteins, that all have a different function in our body, have identical topology: they are the same as an unknotted rope. This means that conventional knot theory is blind to topological features in 97 per cent of the proteins!’
Protein fingerprint
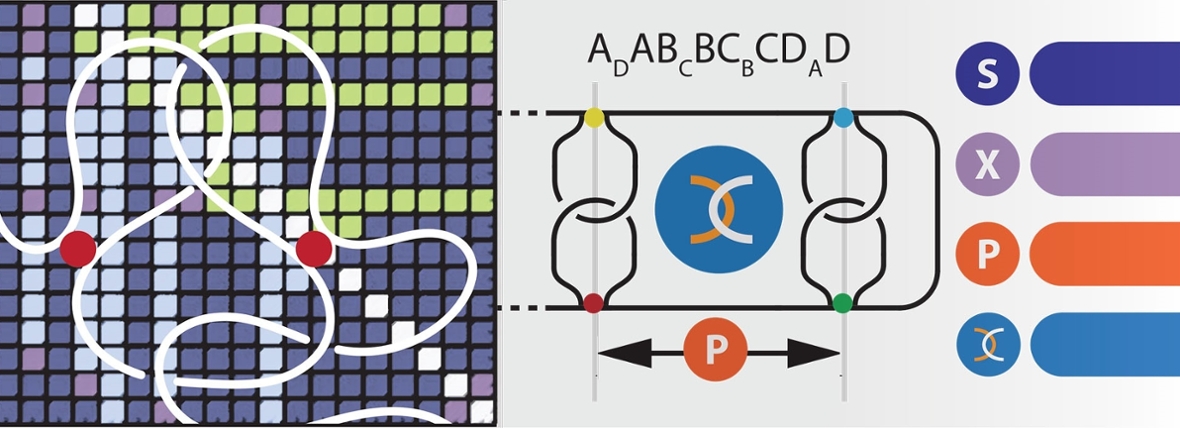
Half a century since Pauling’s prediction, Mashaghi and his team were finally able to solve the problem. They present a new innovative theory called Circuit Topology. This theory not only makes it possible to determine and classify the shape of the majority of proteins, but also to compare their different shapes. In this way, a properly folded protein can be compared to a badly folded one, or proteins can be compared across their evolutionary path. ‘We define the topology of proteins as a simple and precise barcode that allows the identification of all types of folds,’ says Alireza. ‘For this reason, we’d like to call it a protein “fingerprint”.’
Understanding evolution and disease
The topological barcode makes it possible to track the evolutionary changes of proteins and to discover the engineering mechanism of protein. Furthermore, the protein barcode enables the engineering of synthetic proteins for pharmaceutical and industrial applications.
Mashaghi: ‘The new theory will open up new research pathways in the fields of protein physics, protein engineering, evolutionary studies and even genome biology. Protein misfolding is seen especially in neuromuscular diseases as well as some cancers, including breast and prostate cancer, and topological studies may revolutionise the understanding of the disease mechanisms and find new treatments.’
Paper
Anatoly Golovnev & Alireza Mashaghi, Generalized Circuit Topology of Folded Linear Chains, iScience (2020)

What is topology?
Topology is an area of mathematics, which studies how spaces are organised and how they are structured in terms of position. It also studies how spaces are connected. Topology has been called rubber-sheet geometry. In a topology of two dimensions there is no difference between a circle and a square. A circle made out of a rubber band can be stretched into a square. There is a difference between a circle and a figure eight. A figure eight cannot be stretched into a circle without tearing. In the same way, topologists often joke that a donut is the same as a coffee cup.
Further reading
- Maziar Heidari, Helmut Schiessel, and Alireza Mashaghi, Circuit Topology Analysis of Polymer Folding Reactions, ACS Central Science, 6(6): 839–84 (2020)
