
Discovering the physics of banks, the economy and financial crisis
Physicist Diego Garlaschelli co-authored an extensive review in the journal Nature Reviews Physics. Surprisingly, the subject wasn't physics at all, but the networks of banks and other financial institutions, and the way their structure relates to financial crises.
Garlaschelli has pioneered using methods from physics to understand and model financial networks, and the ways their structure can trigger or amplify crises such as the 2008 economic crash. This research, partly in cooperation with De Nederlandsche Bank (DNB), has highlighted early-warning signals of the crisis and better ways of reconstructing, monitoring and crash testing the interbank system. The Nature Reviews Physics publication, reviewing the full field, is a fitting tribute to Garlaschelli's Econophysics and Network Theory group, which is celebrating its 10th birthday this year.

Diego, congratulations on the paper. What have you been trying to oversee with this review?
Together with some of the key scientists in the field, we tried to organize and update the knowledge accumulated over more than two decades of research. Physicists started focusing on financial networks after the 2007-2008 crisis. But a lot of tools had already been developed in the statistical physics community for the analysis and modelling of networks appearing in different disciplines: biological networks, social networks, technological networks like the Internet, and many more.
It all started at the very end of the last millennium, when many influential publications showed that real-world networks arising in diverse contexts share some unique features, irrespective of their details. For instance, in most real-world networks the number of nodes having a certain number of connections typically decreases slowly as this number increases. This means that you can find nodes with vastly different numbers of connections: a few super-connected hubs coexisting with lots of poorly connected nodes.
This striking heterogeneity was unexpected from the network models available in the mathematics literature at that time. Thanks to the appearance of huge new databases, more and more networks started being analysed, showing the same peculiarities. Suddenly, networks became a new object of nature to be studied.
'Naive modelling is one reason why the intensity of the crisis had not been anticipated.'
Additionally, physicists soon realised that the structure of a network has a huge impact on the dynamics of a process taking place on it. In epidemiology, for instance, previous models of disease propagation had relied on very homogeneous models of networks: people gradually infecting only neighbours in their immediate surroundings, as had happened for the Black Death and the other big epidemics.
But modern epidemics, like SARS, Ebola and Covid-19, spread much faster through the airline network, which has a few hubs that can rapidly infect several distant locations. Indeed, another widespread property of real networks is their so-called small world character: any two nodes are on average connected by a short path, even if the network is huge. Based on these observations, network science rapidly revolutionized epidemic modeling.
Then suddenly the financial crisis arrived. The ties, such as loans, among banks turned out to constitute another key network, and one of the main drivers of the dynamics of the crisis, when defaults were cascading through the banking sector. Take a bank that suffers a shock, for instance because its assets suddenly devaluate. If that bank goes default, it will not be able to repay its debt to the other banks it is connected to, and so on, in a cascading process.

Again, it turned out that the architecture of the network has a huge impact on how distress propagates among financial institutions. Basic models used by policy makers and regulators turned out to be unrealistic and not useful in the face of the crisis.
For instance, one of the traditional models used to stress-test the system views each bank as connected to all other banks, so that each of the possible links is realized and assigned a certain average intensity, representing the estimated amount of money in that particular loan.
Real interbank networks turn out to be much sparser, with only a small fraction of links being realized, each with a high intensity, so risk is concentrated in a few but strong links.
If you shock a bank in the first, naive model, it's very unlikely that you can trigger a cascade of defaults, because links are not strong enough to propagate shocks. Every perturbation gets diluted in a sea of links, and the system appears very robust. But in the real world, the few existing strong links can easily propagate shocks. After a few steps, potentially any bank can be reached, due to the small world property.
In the real network and the bad model the properties of individual financial institutions are exactly the same. It’s the way these institutions are connected that dramatically affects the properties of the whole. This is one reason why the intensity of the crisis had not been anticipated.
But how is this (statistical) physics? There are hardly new laws of nature involved.
In physics there are two types of laws of nature: laws that describe how a single, elementary object behaves when it interacts with its surroundings, and laws that describe how several, mutually interacting objects behave collectively. Both types of laws are fundamental and contribute to the same picture, because nature is one, from the small to the large.
Physicists got interested in financial networks when, in the wake of the crisis, researchers and regulators put more emphasis on systemic risk, the collective risk that is embodied by the financial system as a whole and cannot be traced back to traditional risk metrics looking at individual institutions. Collective phenomena are the core focus of statistical physics, the branch of physics that aims to explain the emergent properties of large complex systems of interacting elements.
Another reason why we got interested, is the problem of unobservability of individual links in financial networks: after all, most interbank loans are confidential. So properties crucial to estimate systemic risk must be guessed from partial information.
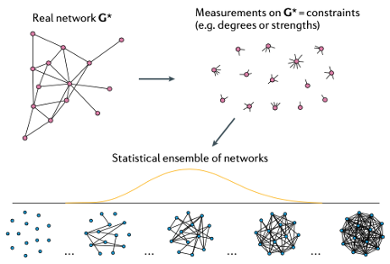
In my group, we realized that a good approach could be the introduction of ensembles of networks, generalizing a technique from statistical physics. When you study a gas, you have a similar problem: you cannot observe the positions and velocities of all particles.
But you can use a macroscopic property, such as the total energy of the gas, as a measurable constraint. Based on that overall constraint, and performing a beautiful conceptual operation grounded in information theory and called entropy maximisation, you can assign probabilities to all the possible configurations of particles that have a certain energy.
This creates a so called ensemble of configurations. Then, you can predict the properties of the system by averaging over the ensemble. This has been hugely successful in physics, so we thought it could work for financial networks as well.
So you're using the toolkit from statistical physics?
Yes. Even though it was not just a matter of taking the tools that already existed and uncritically applying them to a new system. We had to generalise these methods enormously, because the system was much more complicated than a box of particles. Crucially, statistical physics works only if you identify the right constraint.
So we had to realise what a good constraint for financial networks is. Here, the fact that different banks can have very different numbers of connections, and that these numbers are largely stable and characteristic, made us realize that novel ensembles were needed, where constraints are local, which means they are acting on each node of the network separately.
This is something that you normally don’t do in statistical physics, so we had to develop an entire new theory for this, which led to the discovery of entirely new phenomena. We have been exploring this together with mathematicians, especially Frank den Hollander from the Mathematical Institute and other professors involved in the NWO-funded NETWORKS program, and the topic is becoming important in its own right in probability theory.
And how does it work in practice?
There are several financial network reconstruction techniques available. We were surprised to learn that our methods were systematically found, by various independent groups, to outperform other methods. One such group consisted of researchers from several central banks worldwide, including DNB.
Identifying the right theoretical approach was very important, because we had access to very few financial networks to test our own methods. Other teams tested them on more databases they had access to. Clearly, this is confidential information that you cannot easily access. It is a type of study where you cannot release the dataset so that other scientists can reproduce the analysis.
It's even impossible to save the data on your own computers. We could prepare the codes to be run on the servers of the central bank, but then have someone run them for us, and get the results back. Sometimes, students in my group were accepted as interns. With all the signatures and agreements on confidentiality in place, they could run the scripts.
As a physicist, you are used to saying: ‘OK, show me the plot, can you tell me what is that?’ But now I couldn’t see the plot
But you can never talk to them again?
Haha, well let’s say that we had to discuss all the intermediate steps of the analysis in a very uncommon way. As a physicist, you are used to saying: ‘OK, show me the plot, can you tell me what is that?’ But now I couldn’t see the plot, so we had to change our practices a bit.
But in the end, it turned out possible. With other students, I currently have collaborations with the Statistical Office (CBS) and the largest Dutch banks (ING and ABN-AMRO), now focusing on ties between companies. The current corona crisis put emphasis on the role of inter-firm supply networks for the resilience and recovery of the economy. We are therefore generalizing our methods to include new features specific for inter-firm networks.
What do banks get in return for their cooperation?
In all these interactions, I was lucky to find the right people who understand the nature of scientific research. Some of them are mathematicians or physicists by background, and they were very happy of hosting students and collaborating with me, simply for research purposes.
And of course, this research also overlaps with some of the challenges their institutions are facing at the moment. The resilience of the economic system and the stability of financial markets are of concern for DNB as a supervisory authority, and for CBS as a governmental institution supporting policy makers with up-to-date quantitative tools and data, but also for private banks.
For instance, they can improve their risk assessments by complementing the direct information they receive from their clients with the indirect information they acquire if they embed these clients in a network. And they can be better prepared to shocks cascading across different sectors of the economy.
Compared to a university professor, quants in finance get much better salaries. Why don't you switch jobs?
Haha, I like doing research. I’ve really always wanted to be a theoretical physicist, and thinking about new theory is my passion. Actually, I had never suspected I would be involved in applications that practitioners could find useful.
But for me it turned out to be the most rewarding proof of the statement that there is nothing more practical than a good theory. By investigating in depth a new system, you will have to generalise a lot what you already know from physics. You’ll basically have to find new physics.
You need diligent interdisciplinary research and constant interactions with experts in other fields, which is something we strive to foster through the activities of the Leiden Complex Networks Network (LCN2) and the Dutch Network Science Society.
I am excited when I find myself thinking about something new at the fundamentals of statistical physics, by analysing a completely nonphysical system. That is what I really like doing. You're borrowing from physics, but you're also bringing back something genuinely new to physics. Much better than just earning more money, isn’t it?
Marco Bardoscia, Paolo Barucca, Stefano Battiston, Fabio Caccioli, Giulio Cimini, Diego Garlaschelli, Fabio Saracco, Tiziano Squartini, and Guido Caldarelli, "The Physics of Financial Networks", Nature Reviews Physics (2021)
