
Chris Smiet wins Christiaan Huygens prize
Christopher Berg Smiet, who defended his thesis at LION with Dirk Bouwmeester, won the Christiaan Huygens prize for his thesis '‘Knots in Plasma’. On 7 October, he received a certificate, a bronze statuette and ten thousand euros.
‘I really like that such an esoteric subject gets this kind of attention,’ says Chris Smiet. ‘At first sight, this is very abstract mathematics, involving topology and knot theory, but in my field of physics, they turn out to be very much applicable.’
Plasma is a gas-like form of matter in which the electrons have come loose from their atoms. On earth, plasma can be found only in particular places: in fire, tl-lighting, or experimental reactors, but in the wider universe, almost all matter is plasma: stars and the rarified gas between stars.

Tokamaks
‘In a plasma, the electrons and ions (the atoms that lost the electrons) can move independently’, says Smiet. Something extraordinary happens when magnetic fields exist within the plasma: the plasma particles circle around the magnetic field lines, and the upshot of that is that they can move along the field line, but cannot leave it, like beads on a necklace. The plasma is ‘stuck’ on the field lines.
This effect is used in Tokamaks, experimental reactors that contain plasmas at temperatures of hundreds of millions of degrees, by using magnetic fields. The eventual goal is producing energy from nuclear fusion.
Magnetohydrodynamics
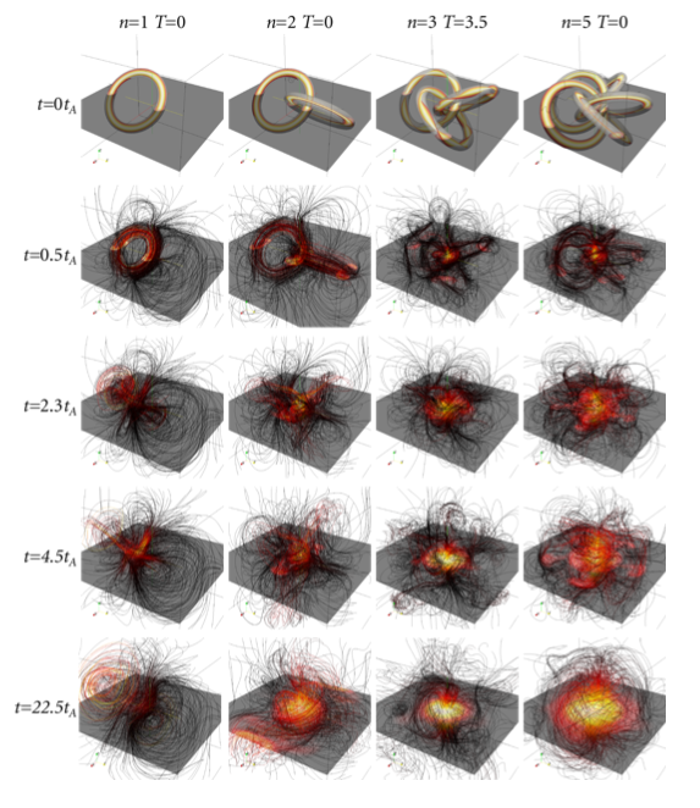
Because the plasma is stuck on the field lines, those cannot cross each other. The lines make stretchable loops that can be linked together like links in a chain.
Predicting how these evolve in time is not easy. The electrical currents along the field lines generate fresh magnetic fields, which in turn cause electrical currents to flow. The resulting intricate pushing and pulling of the plasma particles makes simulations in the field of magnetohydrodynamics notoriously difficult.
Hopf fibration
‘I found out how a configuration of several linked loops will behave’, says Smiet. Using computer simulations and the advanced math fields of knot theory and topology, he discovered that a magnetic plasma knot will evolve toward a stable end configuration, described by the Hopf fibration. ‘This is a very special, extremely elegant knot structure that has been discovered in 1931 by the German mathematician Heinz Hopf.’
In simulations and visualisations, spaghetti-like tangles of field lines are visible, twisted and turned into a donut shape of sorts. Smiets discovery means that it must be possible to make a stable knot of self-contained magnetic plasma, provided that the outside pressure is high enough.
Unlike in tokamaks, where outside magnetic fields control the plasma, this Hopf-tangle would be stable in and of itself. ‘It was a great surprise’, says Smiet, ‘the way that this came out of the mathematics almost by itself.’
Magnetic Plasma knot
This discovery could be helpful, Smiet thinks, in designing reactors for nuclear fusion. But it is also imaginable that Hopf knots already exist, perhaps in the rarified plasma around galaxies.

The Leiden research group of Dirk Bouwmeester is now working on experiments that could create plasma knots in real life, using microwaves and lasers. ‘I have started out as an experimental physicist’, says Smiet, ‘tweaking lasers in the lab. But soon the research veered toward the theoretical. Though I must say, these two are always tightly linked in Bouwmeesters group.’
The Christiaan Huygensprijs has been awarded yearly since 1998 to researchers who have provided an innovative contribution toward mathematics, physics or astronomy. Smiet: ‘I expect there will always be room for new ideas, odd new ways of looking at things.’ Today, Smiet is a postdoc at the Princeton Plasma Physics Laboratory in Princeton, New Jersey, working on the application of his mathematical methods on nuclear fusion reactors.’
