Random walks: wandering the streets like a group of drunk students

01 June 2021

Mathematician Oliver Nagy still vividly remembers the first time he learned about a random walk. ‘The lecturer told us to imagine a company of drunken students who wander in the streets. At each intersection, they would spin one of them around and all would go in the direction where he or she came to a stop.’ In his blogpost on The Network Pages, the reader follows in the footsteps of these intoxicated friends.

A lot of processes in daily life, resemble such a random walk. That is why many mathematicians study them. Nagy: 'By modelling random walks, we can, for example, study stock prices, moving pollen particles, or gambling.’

Lost students

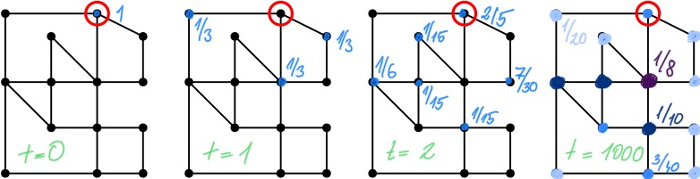
Nagy investigates, for instance, how long it takes before you really lose a drunk group of students. If the group has just left the pub, and there are three intersections down the street, they could be at any one of them with a probability of 1/3. But if you wait too long, they could be just about anywhere in the city. The fact that we know their starting point, will no longer help us - we have lost them.'

Mathematicians speak of reaching the stationary distribution. The time in which the distribution starts to closely resemble its stationary version is called the mixing time. This mixing time is important for physics, cryptography and also for shuffling a deck of cards,' explains Nagy. 'How many shuffles does it take before you have a truly random deck?'

Distribution of the random walk at the start of the walk and then after one, two and way too many steps. The red circle marks the starting position. Blue dots represent the intersections where the random walker may end up being and the numbers next to them represent the probabilities of a random walker being there. In the final figure the probabilities are proportional to the number of streets connected to any given intersection. Different probabilities in this final figure are colour-coded. Credits: Oliver Nagy

Changing streets

A lot has already been said and written about mixing time. Nagy takes it a step further: he looks at what happens to our drunken group of friends when the streets start to change! Think of the stairs at Hogwarts, the school of Harry Potter. The streets move and suddenly lead to a different intersection. What does this do to the mixing time? Will it take longer or shorter before we lose our group of friends?

Nagy explains his findings in his blogpost on The Network Pages - Stumbling around in a changing world

The Network Pages is a website containing information and infotainment about network science. The project was initiated by members and affiliates of the NWO Gravitation grant NETWORKS, but will be open at every level of participation to anyone motivated to contribute.