
Studying abstract mathematical equations using tangible surfaces
On January 5, Rosa Winter will obtain her doctorate in arithmetic geometry. She researched solutions of equations that define so-called ‘del Pezzo surfaces’. ‘I like geometry because I can imagine and draw the shapes and objects,’ says Winter. ‘That makes abstract mathematics feel more tangible.’
In mathematics, it is sometimes useful to study abstract equations using geometric objects, such as circles, spheres, octahedra, or even higher-dimensional objects. The field that connects geometry with abstract equations is called arithmetic geometry. PhD candidate Rosa Winter applied this specific type of geometry in her thesis.
Drawing surfaces
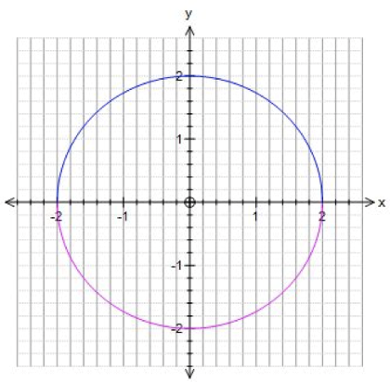
Mathematical equations can define geometric objects, which means that it is possible to study solutions to those equations using geometry. For example, if you want to know which numbers you can enter to make x^2+y^2 equal 4, you can draw all the points (solutions) for which x^2+y^2=4. This results in a circle with radius 2, which shows, for example, that the point x=2, y=0 is a solution. You can also look for specific solutions, like points on the circle where x and y are fractions (1/3rd, 1/5th, but also, 0, 2, etc.). Those fractional solutions are called rational points. Winter studied rational points on surfaces. ‘Surfaces are always two-dimensional, even if they live in eight dimensions,’ says Winter. ‘Which means I can draw surfaces, making the abstract mathematics more intuitive for me.’
Million-dollar question
Finding rational points on geometric objects is rarely easy. This is shown, for example, by the so-called ‘Birch and Swinnerton-Dyer conjecture’. This yet unproven mathematical conjecture is part of the Millennium Prize Problems. The Clay Mathematics Institute awards a million dollars to a correct solution to any of these problems. The conjecture is about rational points on elliptic curves. Like circles, elliptic curves are geometric objects defined by certain equations. When you draw them, they look like curved lines. Winter: ‘Even on elliptic curves, which we know quite a bit about, it is not easy to determine the set of rational points.’
Del Pezzo surfaces
Unfortunately, Winter did not collect the million dollars during her PhD research. She did not work on rational points on elliptic curves, but on so-called ‘del Pezzo surfaces of degree 1’. Winter: ‘From a geometric point of view, these are not the most difficult, most complicated surfaces but they still hold unanswered mathematical questions.’ She showed for part of this family of surfaces that it contains an infinite number of rational points which do not cluster; they can be found scattered around the surfaces. If rational points were visible as red dots and you could walk across such a del-Pezzo surface, you would see red rational points everywhere you look.
Since September, Winter has been working as a postdoc at the Max Planck Institute for Mathematics in the Sciences in Leipzig. Here she learns, among other things, how to apply geometry and abstract mathematics in other sciences, like biology and physics.
Text: Dorine Schenk
