
New scanning method turns objects inside out at high speed
What if you could watch a CT scan live, instead of analysing the images afterwards? If it is up to the Leiden mathematician Jan-Willem Buurlage, that will soon be a reality. He is developing methods to make the algorithms behind 3D scans faster. Quite a challenge: ‘Just like mathematicians, computers are better at thinking than at communicating.’ He defends his thesis on 1 July.
Time consuming
The visualisation of the interior of an object without having to open it up, or: tomography, has a large number of applications,' says Buurlage. 'Think of a patient in a CT scanner, a miniature nanoparticle under a microscope or a bridge that we have to inspect for cracks in the concrete.' This type of reconstruction requires algorithms to combine different 2D images into a single 3D image. However, this step in the reconstruction process is very time consuming, mainly due to the size of the data.
Live report
Buurlage wanted to make this process faster. 'Making a scan and analysing the result are now done separately from each other. First, you make a scan, then you calculate an image of the inside of a patient, for example, and only then are those images studied. As a result, it is not possible to visualise changes inside an object live.'
And that would be very useful: 'If we can already calculate a live image during the scanning process, we can steer the scan during an experiment and, for example, zoom in on a part that looks suspicious or interesting, or prevent unsuccessful recordings by adjusting settings or positions. We can also monitor changes in the object as they happen: you can then, for example, heat a material or let a patient hold his breath.'
Communication problem
To speed up 3D reconstruction, Buurlage uses parallel algorithms. These algorithms use the computing power of multiple computers simultaneously. The computers exchange intermediate results to arrive at the correct answer together. Buurlage: 'This is potentially much faster, but the exchange of information must be done efficiently to prevent the very communication from becoming a bottleneck. In that case, the net profit will not be sufficient'. A big challenge: 'Just like mathematicians, computers are better at thinking than at communicating,' jokes Buurlage.
The result is a solution that avoids linking and therefore communicating between the various calculation elements wherever possible.

Parallel calculations
Problem: You have a collection of unsorted bills of 5, 10, 20 and 50 euros, and you want to know how much you have of each.
Solution 1 (on your own): Go through the stack, and sort the notes into different stacks. Then count the stacks of 5, 10, 20 and 50 euros separately.
Solution 2 ('parallel'): Invite some friends to help you. Give everyone a share of the postage. Everyone performs solution 1 separately on their part of the stack. Then add all the results together to get to the final answer.
A few observations:
- If you only have a few notes, it's quicker to do it yourself instead of dividing the stack.
- If you have a lot of notes, it's faster to call in your friends.
- But suppose you have billions of notes, then you also want to call in millions of people to help you count. Then the last step (adding up all the results to get to the final answer) will be very slow. So you have to try to work around this:
A solution could be to divide everyone into groups. For example: if you make 1,000 groups of 1,000 people, then you have a total of one million counters, but each group only has to add 1,000 intermediate results. Then the intermediate results of each of the thousand groups have to be added up again.
Buurlage's optimisations work according to the same principle, only he doesn't count money, but composes a 3D representation from different images.
Out of the box
But Buurlage also came up with another approach to speed up reconstruction. He explains: 'Normally we first reconstruct the entire 3D image, and then create three cross-sections to visualise it. Also, a live 3D video image would be displayed in this way.'
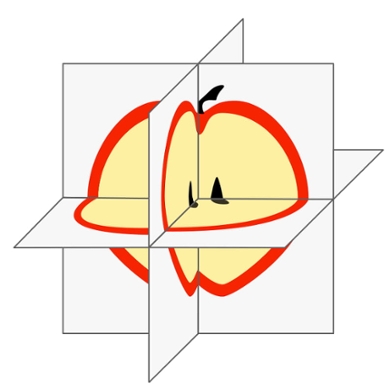
To save time, Buurlage reversed the calculations: he chose three cross-sections and calculated them directly from the data, without reconstructing the entire 3D image first. 'This creates the illusion that we are making a complete 3D reconstruction, while in reality, we are only working with the cross-sections,' says Buurlage. He calls this method quasi-3D.
And that works just fine: 'Even with a normal computer, it takes less than a second to make a high-resolution quasi-3D reconstruction or switch to another section. In follow-up studies, we now also want to improve the image quality and be able to analyse the sections automatically. In the future, we may then be able to automatically detect specific elements, such as a bone fracture or tumour'.
